Investment Portfolio Optimization Techniques: Navigating the thrilling, yet sometimes terrifying, world of finance requires a keen understanding of risk and reward. This exploration delves into the sophisticated strategies employed to maximize returns while mitigating potential losses. From the foundational principles of Modern Portfolio Theory to the cutting-edge applications of machine learning, we’ll uncover the secrets to building a portfolio that not only survives market fluctuations but thrives.
We’ll dissect various optimization methods, including mean-variance analysis and factor-based investing, examining their strengths, weaknesses, and practical applications. Learn how to construct portfolios tailored to different risk tolerances, from the cautious conservative to the daring aggressive investor. Prepare to embark on a journey into the fascinating realm of portfolio optimization, where smart strategies meet savvy decision-making.
Introduction to Investment Portfolio Optimization
Investing wisely isn’t just about throwing darts at a board (though that *could* be surprisingly profitable, statistically speaking). It’s about crafting a portfolio that maximizes your returns while minimizing the risk of losing your hard-earned cash. This involves a fascinating dance between ambition and caution, a tango with the market’s unpredictable moods. Let’s explore the art of portfolio optimization.
Investment Portfolio Optimization Defined
Investment portfolio optimization is the process of constructing an investment portfolio that achieves the highest possible expected return for a given level of risk, or conversely, the lowest possible risk for a given level of expected return. It’s essentially finding the sweet spot between potential gains and the stomach-churning possibility of losses. Think of it as the Goldilocks of finance – not too hot, not too cold, just right.
The Importance of Diversification in Portfolio Construction
Diversification is the cornerstone of a well-optimized portfolio. It’s the age-old adage of “don’t put all your eggs in one basket,” taken to a sophisticated level. By spreading investments across different asset classes (stocks, bonds, real estate, etc.), sectors (technology, healthcare, energy, etc.), and geographies, you reduce the impact of any single investment’s underperformance. Imagine investing solely in a single company, only to have that company’s stock plummet; diversification helps prevent such catastrophic scenarios, acting as a financial safety net. For example, if the tech sector tanks, a diversified portfolio may still see gains from investments in other sectors, preventing a complete portfolio collapse.
The Relationship Between Risk and Return in Portfolio Optimization
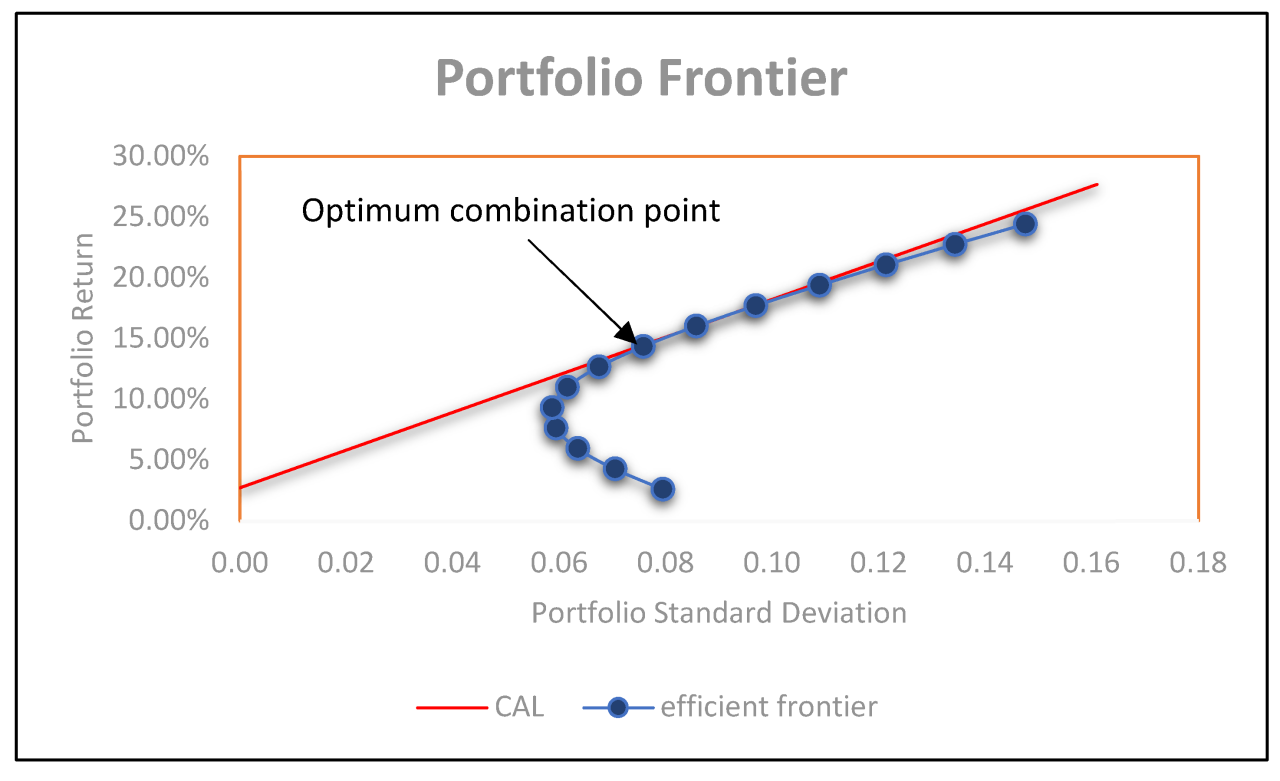
Risk and return are inextricably linked in the world of investing; they’re like two sides of a very shiny coin. Generally, higher potential returns come with higher risk. Investing in a volatile tech startup, for example, could yield enormous profits, but it could also lead to significant losses. Conversely, investing in government bonds typically offers lower returns but carries significantly less risk. Portfolio optimization seeks to find the optimal balance between these two factors based on an investor’s risk tolerance and financial goals. This balance is often visualized using the efficient frontier, a graphical representation of the optimal risk-return combinations. This isn’t some mystical map, but a practical tool to help navigate the financial landscape.
Different Investor Types and Their Risk Tolerances
Investors come in all shapes and sizes, each with their own unique risk appetite. Conservative investors prioritize capital preservation and typically favor low-risk investments like government bonds or high-yield savings accounts. They’re the steady hand on the wheel, preferring a slow and steady approach. Moderate investors seek a balance between risk and return, diversifying their portfolios across a range of asset classes. They’re the sensible navigators, adjusting their course as needed. Aggressive investors are willing to take on higher levels of risk in pursuit of potentially higher returns. These are the thrill-seekers of the investment world, often favoring stocks and other higher-risk investments. Their portfolios are akin to a rollercoaster, offering exciting highs and terrifying lows. The choice of investment strategy depends entirely on an individual’s financial situation, goals, and personal risk tolerance. A young investor with a long time horizon might be more comfortable with aggressive investments, while an investor nearing retirement might prefer a more conservative approach.
Modern Portfolio Theory (MPT)
Modern Portfolio Theory, or MPT, is less a theory and more a gloriously complicated recipe for financial success (or at least, less spectacular failure). It’s the brainchild of Harry Markowitz, a Nobel laureate who clearly understood that investing isn’t just about picking winners; it’s about strategically managing risk across your entire portfolio. Think of it as a sophisticated game of financial Jenga, where you carefully stack assets to build a tower that’s both tall and surprisingly stable.
MPT posits that rational investors focus not only on expected return but also on the risk associated with those returns. It argues that diversification is key—don’t put all your eggs in one basket, unless that basket is lined with gold and guarded by a dragon (in which case, carry on). The core of MPT lies in understanding the relationship between risk and return, allowing investors to construct portfolios that maximize return for a given level of risk, or minimize risk for a given level of return.
The Efficient Frontier: A Map to Financial Utopia
The efficient frontier is the graphical representation of the optimal portfolios that offer the highest expected return for a defined level of risk. Imagine a curved line on a graph, where the x-axis represents risk (usually measured by standard deviation) and the y-axis represents return (usually the expected rate of return). Any portfolio plotting *on* this curve is considered efficient; it provides the best possible return for its level of risk. Points below the curve are inefficient – you could get a better return for the same level of risk by shifting to a point on the curve. Points above the curve are, unfortunately, purely theoretical fantasies.
Calculating Portfolio Variance and Covariance: The Math Behind the Magic
The devil, as they say, is in the details. To construct an efficient portfolio, we need to understand the variance (how spread out the returns of a single asset are) and covariance (how the returns of two assets move together).
Let’s illustrate with a simple example. Imagine a portfolio containing two assets, A and B. Assume asset A has a variance (σ²) of 0.04 and asset B has a variance (σ²) of 0.09. Their covariance (σAB) is 0.02. If we invest 60% in asset A and 40% in asset B, the portfolio variance (σp²) is calculated as follows:
σp² = wA²σA² + wB²σB² + 2wAwBσAB
Where: wA and wB are the weights of assets A and B respectively.
Substituting our values:
σp² = (0.6)²(0.04) + (0.4)²(0.09) + 2(0.6)(0.4)(0.02) = 0.0336
The portfolio standard deviation (σp), which is the square root of the variance, represents the portfolio risk. In this case, σp = √0.0336 ≈ 0.183. This calculation demonstrates how diversification, through careful selection of assets with lower covariance, can reduce overall portfolio risk.
A Hypothetical MPT Portfolio: Building a Better Mousetrap (for Money), Investment Portfolio Optimization Techniques
Let’s create a hypothetical portfolio using MPT principles. We’ll consider three asset classes: Large-cap stocks (representing higher growth potential and higher risk), government bonds (representing lower growth potential and lower risk), and real estate (offering a moderate risk/reward profile).
We’ll assume the following (highly simplified) expected returns and standard deviations:
| Asset Class | Expected Return | Standard Deviation |
|---|---|---|
| Large-cap Stocks | 10% | 15% |
| Government Bonds | 3% | 5% |
| Real Estate | 6% | 10% |
(Note: These are illustrative figures and do not reflect actual market conditions. Real-world MPT involves much more complex calculations and data.)
Using optimization techniques (beyond the scope of this explanation, but readily available in financial software), we might arrive at an optimal portfolio allocation of approximately 60% Large-cap stocks, 25% Real Estate, and 15% Government Bonds. This allocation aims to balance the higher potential return of stocks with the stability of bonds and the moderate return of real estate, achieving a desirable risk-return profile for the investor. The exact allocation would depend on the investor’s risk tolerance and the specific covariance matrix of the assets.
Mean-Variance Optimization
Mean-variance optimization, darling, is the heart and soul of portfolio construction for the financially sophisticated (and slightly neurotic). It’s a mathematical approach that aims to find the optimal portfolio allocation – the perfect mix of assets – by balancing the expected return (the mean) against the risk (the variance). Think of it as a delicate dance between greed and fear, all quantified and neatly packaged into an equation.
The process, while elegant in theory, is delightfully complex in practice. First, you need to estimate the expected return and variance of each asset in your universe. This involves peering into the crystal ball of the market, a feat that even the most seasoned soothsayers struggle with. Then, you use these estimates (along with the correlations between assets – how much they wiggle together) to create a model. This model then crunches the numbers to find the portfolio that maximizes return for a given level of risk, or minimizes risk for a given level of return. It’s like finding the sweet spot on a rollercoaster: maximum thrills with minimal stomach-churning.
Mean-Variance Optimization Models
Several different models exist to perform this mean-variance magic. The simplest is the Markowitz model, the granddaddy of them all, which directly applies the mean-variance framework. However, more sophisticated models have emerged to address some of the inherent limitations of the basic approach. These include methods that incorporate constraints (like limiting exposure to specific sectors or asset classes) or use robust estimation techniques to handle uncertainty in the input data. These advanced models are like adding seatbelts and airbags to our rollercoaster – enhancing safety and reliability.
Limitations of Mean-Variance Optimization
While mean-variance optimization sounds like a financial panacea, it’s not without its flaws. One major limitation is its reliance on historical data to predict future returns and volatilities. As anyone who’s ever invested knows, the past is not always a reliable predictor of the future. It’s like using last year’s weather forecast to plan this year’s picnic – risky business! Furthermore, the model assumes that returns are normally distributed, which isn’t always the case. Fat tails, those pesky outliers that can wipe out your portfolio in a flash, are often ignored. Finally, the model is highly sensitive to the inputs. Slight changes in estimated returns or volatilities can lead to dramatically different optimal portfolios. It’s a bit like building a house of cards – a slight breeze can bring the whole thing tumbling down.
Comparison of Mean-Variance Optimization Methods
| Method | Description | Advantages | Disadvantages |
|---|---|---|---|
| Markowitz Model | Basic mean-variance optimization | Simple, foundational | Sensitive to input errors, assumes normal distribution |
| Black-Litterman Model | Incorporates investor views | Allows for subjective input, more robust | Requires careful calibration of investor views |
| Robust Optimization | Handles uncertainty in input data | Less sensitive to estimation errors | Can lead to more conservative portfolios |
| Resampled Efficient Frontier | Uses Monte Carlo simulation to account for estimation uncertainty | Provides a range of optimal portfolios | Computationally intensive |
Factor-Based Investing: Investment Portfolio Optimization Techniques
Forget chasing individual stocks like a caffeinated squirrel; factor-based investing is about identifying and exploiting systematic market patterns. Instead of picking winners based on gut feeling (or a particularly insightful horoscope), it leverages the power of statistically significant factors to build a portfolio. Think of it as a more sophisticated, less chaotic approach to market prediction—though, let’s be honest, predicting the market is a fool’s errand, but this makes it a *slightly less foolish* errand.
Factor investing posits that certain characteristics or factors consistently predict higher returns over the long haul. By identifying these factors and tilting your portfolio towards them, you aim to capture these excess returns, rather than relying on individual stock picking, which is more akin to darts thrown blindfolded at a stock ticker. This approach emphasizes identifying and exploiting these market anomalies, often based on historical data, rather than solely on individual stock valuations. It’s less about predicting the future and more about capitalizing on historical tendencies.
Common Factors in Factor-Based Investing
Several factors have consistently shown a link to higher returns. Understanding these factors is crucial for crafting a successful factor-based strategy. These factors aren’t guaranteed to work forever—market dynamics are notoriously fickle—but historically, they’ve offered a statistical edge. Think of it as playing the odds, not guaranteeing a win.
Examples of Factor-Based Investment Strategies
Let’s ditch the theoretical and delve into some real-world examples. Imagine constructing a portfolio heavily weighted towards small-cap stocks (a size factor strategy), or one focusing on companies with high book-to-market ratios (a value factor strategy). A momentum strategy might concentrate on stocks that have shown strong price appreciation recently, betting that this trend will continue (at least for a while). These are not guarantees, of course, just statistically-supported bets. Remember, past performance is not indicative of future results, but in factor investing, we’re banking on statistically significant historical patterns. Another example could be a low-volatility strategy, which selects stocks that have exhibited lower price fluctuations than the market average. This aims to minimize risk while potentially sacrificing some upside.
Factor-Based Investing vs. Traditional MPT: A Comparison
| Feature | Factor-Based Investing | Modern Portfolio Theory (MPT) |
|---|---|---|
| Focus | Exploiting systematic risk factors | Diversification to minimize risk |
| Asset Selection | Based on factor exposures | Based on individual asset risk and return |
| Risk Management | Factor risk exposures are managed | Portfolio variance is minimized |
| Performance | Aims for consistent outperformance through factor premiums | Aims for optimal risk-adjusted returns |
Risk Management Techniques
Investing is a thrilling rollercoaster, a financial equivalent of a particularly spicy jalapeno popper – exhilarating, but potentially fiery. To navigate this exhilarating yet precarious landscape, a robust risk management strategy is not merely advisable, it’s practically mandatory. Without it, your portfolio could go from a spicy delight to a full-blown inferno. Let’s explore the tools and techniques that can help you tame the volatility beast.
Risk management in portfolio optimization isn’t about avoiding risk entirely – that’s akin to refusing to eat because some peppers might be too hot. Instead, it’s about intelligently identifying, measuring, and mitigating potential downsides while maximizing potential upsides. This involves a multi-faceted approach incorporating various techniques, each playing a crucial role in safeguarding your investment.
Stress Testing and Scenario Analysis
Stress testing and scenario analysis are like running “what if” simulations on your portfolio’s resilience. Instead of simply assuming a smooth, predictable market, these techniques subject your portfolio to extreme market conditions – a sudden economic downturn, a sharp rise in interest rates, or a geopolitical crisis. By observing how your portfolio performs under these stressful scenarios, you can identify potential weaknesses and adjust your strategy accordingly. For example, a stress test might simulate a 30% market crash to see how your portfolio holds up, revealing if you have sufficient diversification or need to adjust your asset allocation. Scenario analysis, on the other hand, allows for a more nuanced approach, exploring various combinations of market factors and their potential impact on your portfolio. Think of it as a detailed war game for your investments.
Hedging and Derivatives
Hedging is like buying an insurance policy for your investments. It involves using financial instruments, such as derivatives, to offset potential losses from adverse market movements. For example, if you own a significant amount of stocks in a particular sector and fear a downturn, you might use futures contracts to hedge against potential losses. Derivatives, such as options and futures, are powerful tools but should be used cautiously, as they carry their own risks. Misusing them can amplify losses rather than mitigate them. Imagine trying to extinguish a fire with gasoline – not the most effective strategy. Therefore, a thorough understanding of these instruments and their inherent risks is essential.
Value at Risk (VaR)
Value at Risk (VaR) is a statistical measure that quantifies the potential loss in value of an asset or portfolio over a specific time horizon and confidence level. It answers the question: “What is the maximum loss I can expect to experience with a given probability?” For example, a VaR of $10,000 with a 95% confidence level over a one-month period means there’s a 5% chance that your portfolio will lose more than $10,000 in one month. VaR is a widely used risk management tool, but it’s important to remember that it’s just a statistical estimate, and actual losses could exceed the VaR calculation. Think of it as a weather forecast – it provides a probability, but there’s always a chance of unexpected storms.
Portfolio Rebalancing Strategies
Rebalancing your investment portfolio might sound like a chore – like weeding your financial garden – but it’s a crucial step in maintaining your desired asset allocation and potentially boosting your returns. Think of it as regularly pruning your portfolio to keep it healthy and prevent any one plant (asset class) from overshadowing the others. Ignoring this crucial task can lead to unwanted imbalances and increased risk, much like letting your garden grow wild.
Rebalancing involves adjusting your portfolio’s asset allocation back to your target percentages after market fluctuations cause deviations. This disciplined approach helps you capitalize on market dips and avoid overexposure to any single asset class that may be performing exceptionally well (and thus, potentially due for a correction).
Time-Based Rebalancing
Time-based rebalancing follows a predetermined schedule, regardless of market performance. For example, an investor might rebalance their portfolio annually, semi-annually, or even quarterly. This approach offers simplicity and consistency, making it ideal for investors who prefer a “set it and forget it” strategy. However, it can lead to frequent trading if market volatility is high, potentially increasing transaction costs. Consider a scenario where an investor’s portfolio is significantly out of balance due to a sudden market downturn. A time-based rebalancing approach would trigger a purchase of assets that have declined in value, a strategy often advocated by value investors.
Level-Based Rebalancing
Level-based rebalancing, on the other hand, triggers rebalancing only when the portfolio deviates from the target allocation by a certain percentage. This approach is more reactive to market movements, allowing investors to capitalize on significant shifts. For instance, an investor might rebalance when any asset class drifts more than 5% from its target weight. This strategy minimizes transaction costs by only rebalancing when necessary. However, it requires more active monitoring of the portfolio. Let’s imagine a stock within the portfolio experiencing a substantial surge. A level-based approach would wait until the deviation reaches the predetermined threshold before selling some of that winning stock to realign with the target allocation.
Comparison of Rebalancing Approaches
Time-based rebalancing provides predictability and simplicity, but can lead to higher transaction costs and potentially less optimal buying and selling opportunities. Level-based rebalancing is more responsive to market fluctuations, minimizing transaction costs, but requires more active management and attention. The choice between these methods depends on individual investor preferences, risk tolerance, and investment goals. Ultimately, there’s no universally “best” strategy; it’s a matter of finding the approach that best suits your personal circumstances and investment philosophy.
Factors Influencing Rebalancing Frequency
Several factors influence how often an investor should rebalance their portfolio. These include:
- Investment Goals: Long-term investors may rebalance less frequently than short-term investors.
- Risk Tolerance: Investors with higher risk tolerance might rebalance less frequently, while those with lower risk tolerance may rebalance more often.
- Market Volatility: High market volatility may necessitate more frequent rebalancing to maintain the desired asset allocation.
- Transaction Costs: High transaction costs might discourage frequent rebalancing.
- Tax Implications: Tax implications of frequent trading should be considered.
Implementing a Rebalancing Strategy: A Step-by-Step Guide
A well-defined process is essential for successful portfolio rebalancing.
- Define your target asset allocation: Determine the desired percentage allocation for each asset class (e.g., stocks, bonds, real estate).
- Choose a rebalancing strategy: Select either a time-based or level-based approach, considering your risk tolerance and investment goals.
- Monitor your portfolio regularly: Track the performance of your assets and their deviation from the target allocation.
- Calculate the necessary adjustments: Determine the amount of each asset to buy or sell to return to the target allocation.
- Execute the trades: Implement the necessary transactions to rebalance your portfolio.
- Document the rebalancing: Keep records of all rebalancing activities for tax purposes and performance tracking.
Advanced Portfolio Optimization Techniques

So, you’ve mastered the basics of portfolio optimization – congratulations, you’re officially less likely to accidentally invest your life savings in Beanie Babies 2.0! But the world of portfolio optimization is far from a neatly arranged spreadsheet. Let’s delve into the more sophisticated strategies that can help you navigate the wild, wild west of finance. Prepare for some seriously advanced number-crunching – and maybe a mild existential crisis about the inherent unpredictability of markets.
Black-Litterman Model
The Black-Litterman model offers a clever way to improve upon the limitations of traditional mean-variance optimization. Instead of relying solely on historical data (which can be notoriously fickle), this model allows you to incorporate your own views, or “views,” about specific assets or market factors. This is like adding your own spice to the pre-made portfolio sauce – you get a more personalized and potentially more profitable result. For example, if you believe that a particular technology sector is poised for explosive growth, you can input this “view” into the model, which will then adjust the portfolio allocation accordingly, taking into account both your expertise and the historical data. This elegantly combines the wisdom of crowds (historical data) with the brilliance of your own market insights (your views). The mathematical underpinnings involve Bayesian updating, which essentially allows for the blending of prior beliefs (historical data) with new information (your views).
Stochastic Programming in Portfolio Optimization
Forget the neat, deterministic world of perfectly predictable returns. Stochastic programming embraces the reality of uncertainty. This technique uses probability distributions to model the uncertain future returns of assets. Instead of optimizing for a single, fixed scenario, stochastic programming aims to find a portfolio that performs well across a range of possible future outcomes. Think of it as building a portfolio that can withstand a variety of economic storms, rather than one perfectly tailored to a calm, sunny day. A classic example would involve modelling the probability of different economic scenarios (e.g., recession, expansion) and their impact on asset returns. The optimization then aims to find a portfolio that minimizes the expected loss across these various scenarios.
Machine Learning Applications in Portfolio Management
Machine learning is no longer a futuristic fantasy; it’s becoming increasingly commonplace in portfolio management. Algorithms can analyze vast datasets, identify complex patterns that humans might miss, and make predictions about future market movements. This is where the fun begins, as we can employ algorithms such as Support Vector Machines (SVMs) for classification tasks (like identifying undervalued stocks), or neural networks for regression tasks (like predicting future asset prices). For example, a machine learning model might analyze thousands of company reports, news articles, and social media posts to identify stocks likely to outperform the market. However, it’s crucial to remember that even the most sophisticated algorithms are not crystal balls; they require careful monitoring and validation. One needs to account for the potential for overfitting and model drift, which could lead to disastrous results if not properly addressed.
Hypothetical Portfolio Design Using Advanced Optimization
Let’s imagine we’re using a Black-Litterman model to construct a portfolio. We start with a traditional mean-variance optimized portfolio based on historical data. Then, we incorporate our “view” that emerging market equities will outperform developed market equities over the next five years. The Black-Litterman model will adjust the portfolio allocation, increasing the weighting of emerging market equities and potentially reducing the allocation to developed market equities, reflecting our view while still considering the historical data and its inherent uncertainties. The specific allocation will depend on the strength of our view (how confident we are in our prediction) and the uncertainty associated with the historical data. For instance, if our view is very strong and we are highly confident in our prediction, the portfolio will shift significantly towards emerging market equities. However, if our view is weaker or we have less confidence, the shift will be more moderate. The final portfolio would then be a carefully balanced blend of historical data-driven allocations and our expert insights. This process can be repeated with multiple views, allowing for a highly customized and nuanced portfolio allocation strategy.
Illustrative Examples of Optimized Portfolios
Let’s ditch the theoretical mumbo-jumbo and dive into the real world of portfolio optimization. We’ll examine two contrasting portfolios, one for the cautious turtle and another for the daring hare, showcasing how different risk tolerances lead to vastly different investment strategies. Remember, these are illustrative examples and not financial advice – consult a professional before making any investment decisions. Investing is serious business, folks, not a game of chance (though it can feel like one sometimes!).
To effectively illustrate the principles of portfolio optimization, we’ll create two distinct portfolios: one tailored for a conservative investor seeking capital preservation and steady, albeit modest, returns, and another geared towards an aggressive investor aiming for substantial growth, accepting higher volatility along the way. We’ll analyze their composition, risk-return profiles, and key characteristics to demonstrate the practical application of the optimization techniques discussed previously.
Conservative Investor Portfolio
This portfolio prioritizes capital preservation and steady income generation over aggressive growth. Think of it as a comfortable, well-worn armchair rather than a thrilling rollercoaster ride. It leans heavily on lower-risk asset classes to minimize potential losses. A significant portion is allocated to government bonds and high-quality corporate bonds, providing a predictable stream of income and a relative safety net against market fluctuations. A smaller allocation is dedicated to dividend-paying stocks known for their stability and consistent payouts, offering a blend of income and modest growth potential. Finally, a small allocation to a diversified real estate investment trust (REIT) adds some diversification and inflation hedging.
- Asset Allocation: 60% Government Bonds, 30% High-Quality Corporate Bonds, 5% Dividend-Paying Stocks, 5% REITs
- Expected Return: 4-6% annually
- Risk Tolerance: Low
- Investment Horizon: Long-term (10+ years)
Aggressive Investor Portfolio
This portfolio embraces risk to pursue higher returns. Think of it as a Formula 1 car, built for speed and performance but requiring a skilled driver and a tolerance for bumps in the road. A significant portion is allocated to growth stocks, particularly those in rapidly expanding sectors like technology and renewable energy. These investments offer the potential for substantial gains but also carry a higher risk of significant losses. A smaller allocation is dedicated to emerging market equities, which can offer even higher growth potential but with increased volatility. A modest allocation to alternative investments, such as venture capital or private equity (if accessible), provides further diversification and potentially higher returns, though with significantly higher risk.
- Asset Allocation: 40% Growth Stocks, 30% Emerging Market Equities, 20% Small-Cap Stocks, 10% Alternative Investments (if accessible)
- Expected Return: 8-12% annually (with higher volatility)
- Risk Tolerance: High
- Investment Horizon: Long-term (10+ years)
Comparison of Conservative and Aggressive Portfolios
The following table summarizes the key differences between these two portfolios:
| Characteristic | Conservative Portfolio | Aggressive Portfolio |
|---|---|---|
| Asset Allocation | Predominantly fixed-income and low-risk equities | Significant allocation to growth stocks and higher-risk assets |
| Expected Return | Lower, but more stable | Higher, but more volatile |
| Risk | Low | High |
| Suitability | Risk-averse investors with long-term horizons | Risk-tolerant investors with long-term horizons and higher risk tolerance |
Conclusive Thoughts
Mastering Investment Portfolio Optimization Techniques is not about predicting the future; it’s about strategically positioning yourself for success, regardless of what the future holds. By understanding the principles of diversification, risk management, and sophisticated optimization models, investors can significantly enhance their chances of achieving their financial goals. Remember, a well-optimized portfolio is more than just a collection of assets; it’s a carefully crafted strategy designed to navigate the complexities of the market and secure a prosperous financial future. So, go forth and optimize!
FAQ Corner
What’s the difference between active and passive portfolio management?
Active management involves actively trying to beat the market through stock picking and market timing. Passive management involves mirroring a market index, aiming for market-average returns with lower fees.
How often should I rebalance my portfolio?
Rebalancing frequency depends on your investment goals and risk tolerance. Common approaches include annual, semi-annual, or even quarterly rebalancing.
Can I use portfolio optimization techniques for retirement planning?
Absolutely! Portfolio optimization is crucial for retirement planning, helping to balance risk and return based on your retirement timeline and desired income stream.
What are some common mistakes to avoid in portfolio optimization?
Common mistakes include over-diversification, ignoring fees, emotional decision-making, and failing to regularly review and rebalance your portfolio.